6  Analysis of Variance

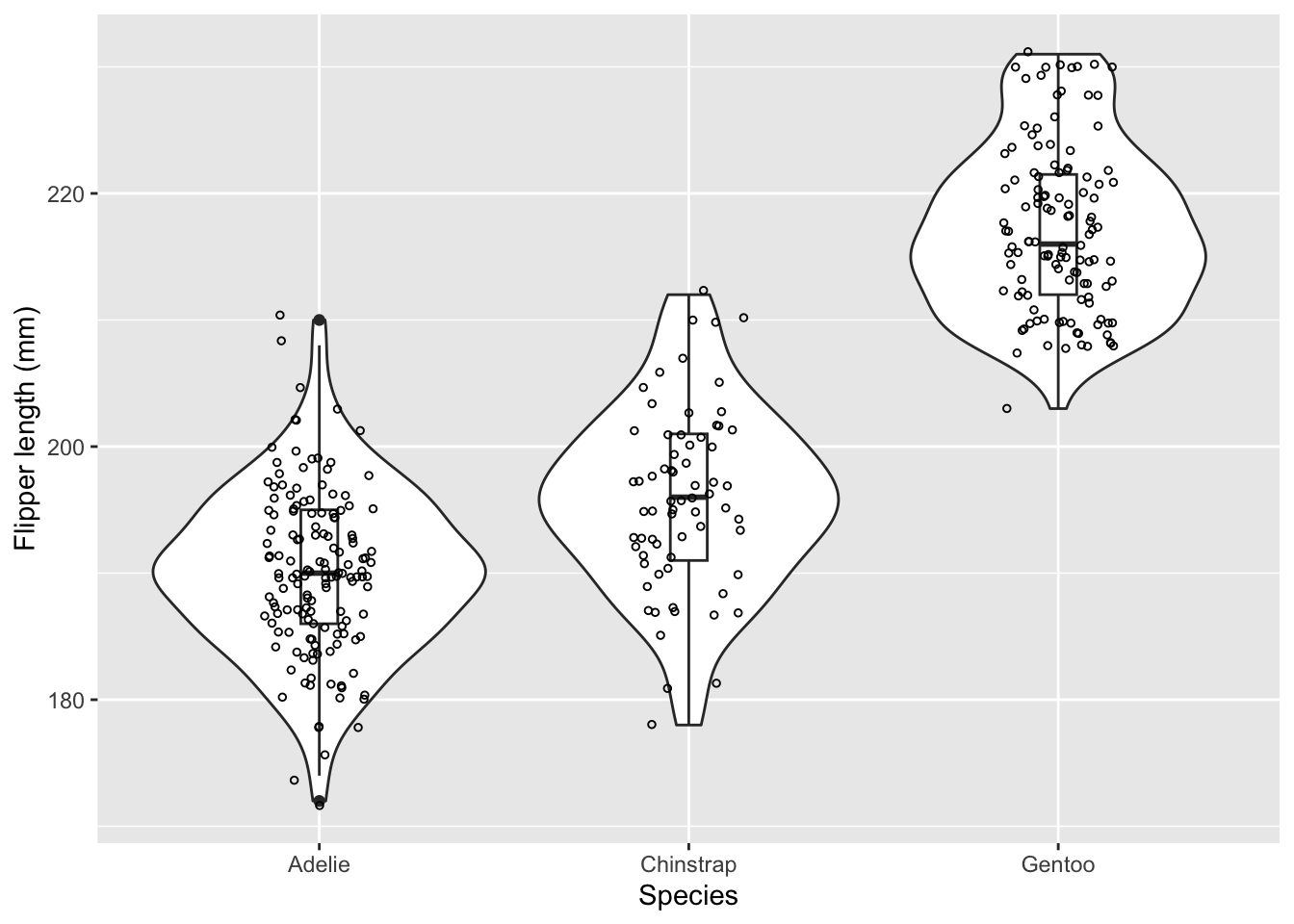
An ANOVA test with two groups is equivalent to a two-sample t-test. Unlike two-sample t-tests, ANOVA can simultaneously test many groups without inflating the Type I error rate beyond \(\alpha\).

Here is an example of using ANOVA to test whether the mean flipper length is different between three different species of penguins.

6.1 Visualizing data

Since we have large sample sizes, it would be helpful to visualize the data with a violin plot (or a boxplot would work too).

palmerpenguins %>%
  ggplot(aes(x = species, y = flipper_length_mm)) +
  geom_violin() +
  geom_boxplot(width = 0.1) +
  geom_jitter(size = 1, shape = 1, width = 0.15) +
  xlab('Species') +
  ylab('Flipper length (mm)')

6.2 Hypotheses

The null hypothesis for an ANOVA test is that the population means, \(\mu_i\), are the same for all treatments. The alternate hypothesis is that at least one population mean is different from the rest. ANOVA cannot give us information about which group’s population mean is different from the rest.

  • \(H_0\): Mean flipper length is equal among all three species (\(\mu_1 = \mu_2 = \mu_3\)).
  • \(H_A\): At least one species’ mean flipper length is different from the rest.

We’ll be conducting a fixed-effects ANOVA test, which uses the F-test statistic.

6.3 Checking assumptions

ANOVA makes the same assumptions as a two-sample t-test:

  • Both samples represent random samples obtained from their populations.
  • The variable in question is normally distributed in each population.
  • The variance of the variable is the same in each population.

We can check the normality assumption using a normal quantile plot:

palmerpenguins %>%
  ggplot(aes(sample = flipper_length_mm)) +
  stat_qq(shape = 1) +
  stat_qq_line() +
  facet_grid(~ species) +
  xlab('Normal quantile') +
  ylab('Flipper length (mm)')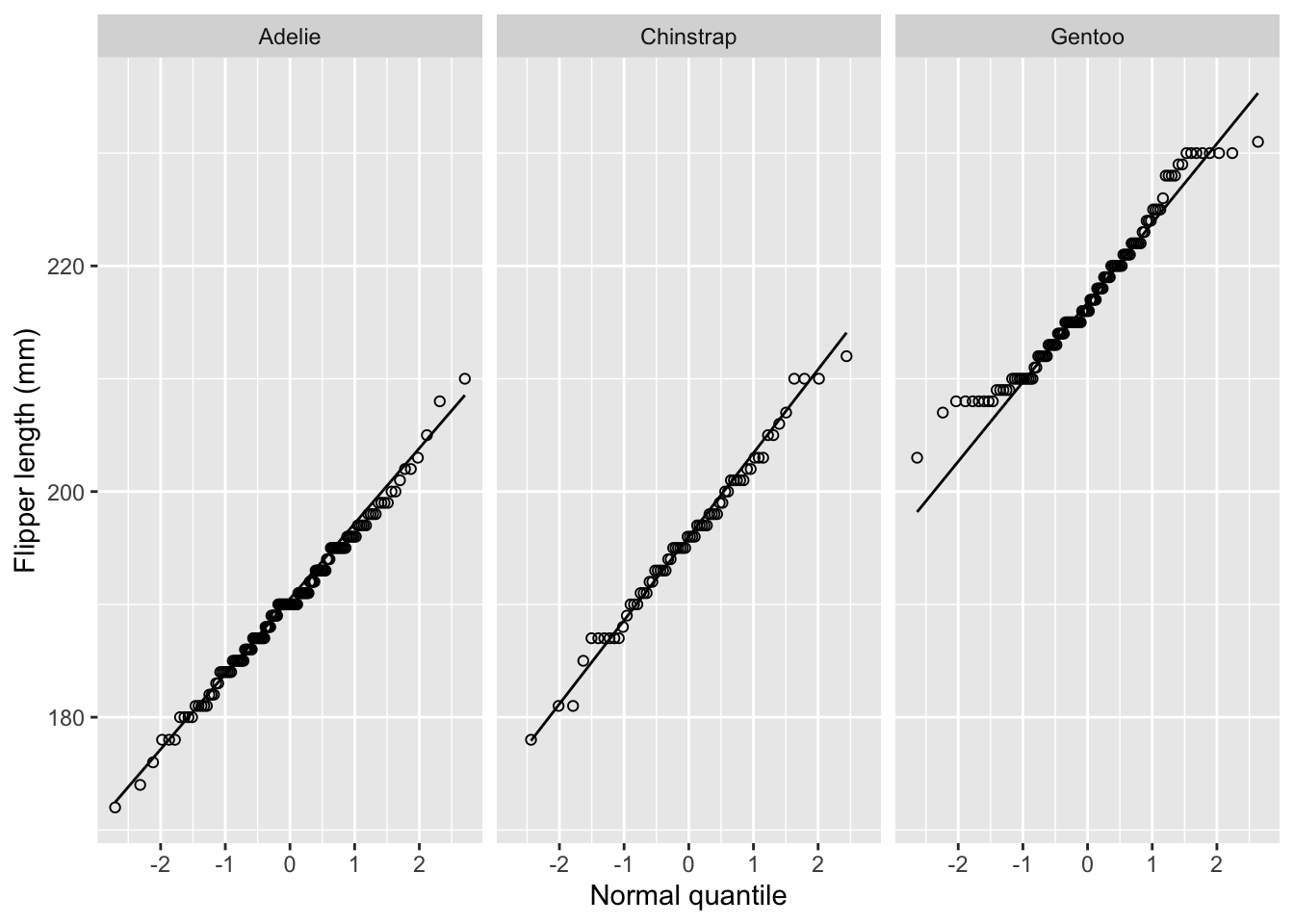

We can check the homoscedasticity (equal variances) assumption using the Bartlett’s test:

bartlett.test(flipper_length_mm ~ species, data = palmerpenguins)

    Bartlett test of homogeneity of variances

data:  flipper_length_mm by species
Bartlett's K-squared = 0.80702, df = 2, p-value = 0.668

Since the P-value is greater than 0.05, we fail to reject the null hypothesis of equal variances.

6.4 Performing an ANOVA test

There are two steps to performing an ANOVA test in R. First, we need to create a linear model using the lm function. Then, we can pass that to the anova method to generate the appropriate ANOVA results.

palmerpenguins.lm <- lm(flipper_length_mm ~ species, data = palmerpenguins)
anova(palmerpenguins.lm)
Analysis of Variance Table

Response: flipper_length_mm
           Df Sum Sq Mean Sq F value    Pr(>F)    
species     2  50526 25262.9  567.41 < 2.2e-16 ***
Residuals 330  14693    44.5                      
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
\(df\) Sum of Squares Mean of Squares \(F\)-ratio \(P\)
Species 2 50526 25262.9 567.41 2.2e-16
Residuals 330 14693 44.5

Due to the low P-value, we can reject the null hypothesis that the mean flipper length is equal. But now the question is, which group mean(s) differ?

6.5 Post-hoc Tukey

The Tukey-Kramer post-hoc test (yes, a mouthful) compares all group means to all other group means. This is preferable to doing multiple two-sample t-tests because the latter inflates the Type I error rate.

To conduct this test in R, we first need to re-do the ANOVA test using the aov method and pass that onto TukeyHSD(). An example is shown below:

aov(flipper_length_mm ~ species, data = palmerpenguins) %>%
  TukeyHSD(conf.level = 0.95)
  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = flipper_length_mm ~ species, data = palmerpenguins)

$species
                     diff       lwr       upr p adj
Chinstrap-Adelie  5.72079  3.414364  8.027215     0
Gentoo-Adelie    27.13255 25.192399 29.072709     0
Gentoo-Chinstrap 21.41176 19.023644 23.799885     0